Permutation and combination

Guess who almost forgot to blog again! THIS GIRL. Anyway i cant reach my laptop so im on my ipad and apologize for any spelli issues. Okay so this week we did permutation and combination. These are two types of probability that basically tell you how things can be put into order.

Permutation is used when order is important. For instance, if you need to elect a president, vice president, and secretary to the student council but you have 30 members you would use permutation. There is an equation for this, but it is in my locker at school. So in a bit I will teach you how to use the calculator buttons.

Combination is used when order is completely and totally irrelevant. For instance, if you needed to elect three officers to a student board of thirty students combination would be used. Oh and by the way both of these involve factorials. There is an equation for this too. That is also in my locker.

EXAMPLE: You have choose 44 cards from a standard 52 card deck. The order of the cards you choose is irrelevant.

For this problem, you would use combination. Set up the equation 52C44 the big number always comes first.

Then pull out your handy dandy calculator. Type in the first number. Press the math key, go over to the last little column and select the combination button. Type the second number. Press enter. Write the answer on the paper.

Anyway this particular answer is...hang on I have to change the batteries in my calculator...752538150. That's how you do that.

I hope you've all enjoyed the most impromptu blog ever written. Okay goodnight.

--Sarah

permutations and combinations

k today im teaching you how to do permutations and combinations. it is a really easy process if you know what you are doing. you use permutation if the order is important and you use combination if the order is not important. for permutation you use the formula:   n! / (n-r)! or nPr. for combination you use the formula:       n! / (n-r)! r! or nCr. so i will provide an example below to show you exactly what all this means.


EX:
a) in how many ways can a club with 20 members choose a president, vice president, secratary
b) in how many ways can they choose a 4 person govering council
 

a)order does matter because it is three different ranks
so it is nPr
plug in numbers
20 P 3--- 3 because pres, vice pres and sec
20! / (20-3)!
= 20! / 17!
17! cancels and leaves you with 20*19*18 = 6840 ways

b)order does not matter because positions are all the same
so its is nCr
plug in
20 C 4
20! / (20-4)! 4!
20! / 16! 4!
16! cancels so you are left with 20*19*18*17 / 4*3*2*1 = 4845 ways

Permutations and Combinations

This week we learned about permuatations and combinations. Permutationa and combinations are formulas used to find different ways something can be ordered. The difference between a permutation and combination is that you use a permutation when the order is important and you use a combination when the order is NOT important.

Some things to know:

• 
  
  The formula for a permutation is n!/(n-r)!


• 
  
  The formula for a combination is n!/(n-r)r!


• 
  
  Your n will ALWAYS be larger than you r.

Let's do some examples to help you better understand.

Example 1: 5P3

5P3=5!/(5-3)!

=5!/2!

=5*4*3*2*1/2*1

= 60

Example 2: 5C3

5C3=5!/(5-3)3!

=5!/2!3!

=5*4*3*2*1/2*1*3*2*1

=20/2

=10

And there you have it(:

Permutations and Combinations

This weekend I am going to teach you all how to work problems that involve permutations and combinations. These are probability problems. Before I show you an example, there are a few things that you need to know about permutations and combinations.

Notes:
• You use permutation when the order is important
• You use combination when the order is not important
• nPr = (n!)/(n-r)! is the formula for permutation
• nCr = (n!)/(n-r)!r! is the formula for combination
• n will always be the larger number in a permutation or combination problem
• These problems can also be solved by inputting the information into your calculator

Example: In how many ways can a organization with 15 members choose 5 different officers?
• All of the officers are different, so that means that the order is important. You would use permutation for this problem.
• So n=15 and r=5, 15P5
• Your final answer would be 360,360

-Braxton

Permutations and Combinations

ok so today im going to talk about permutation and combination. In order to do these problems you will need to know a few things.

Permutation is used when you need to find out how many different ways something can be ordered when order is important! The formula for Permutation is:

• nPr = n!/(n-r)!

Combination is used when you need to find out how many different ways something can be ordered when order is NOT important! The formula for Combination is:

• nCr = n!/(n-r)!r

Now that i have given you some info about this.

Example 2: In how many ways can you choose 4 marbles from a bag of 20 marbles if the color does not matter?

• Since the question says "does not matter", we know that we should use combination.
• Formula: nCr = n!/(n-r)!r!
• 20C4 = 20!/(20-4)!4! = 20!/16!4! = 20 x 19 x 18 x 17/4 x 3 x 2 x 1 = 116280/24 = 4845

Bam! all done!

Combination and Permutation

Okay, so this week I am going to explain how to work problems using combination and permutation. This is extremely easy. First your going to need to know a few things.

• You use combination when order does't matter
• You use permutation when order does matter
• The formula for combination is nCr = n!/(n-r)!r!
• The formula for permutation is nPr = n!/(n-r)!
• Another way to work these problems out is by using the combination or permutation function in your calculator.
• n is always going to be the bigger number, while r is always going to be the smaller number in the word problems.

Okay, so now that you know all that you need to know i guess ill work a few examples for you.

example 1: In how many ways can a club with 13 members choose 4 different officers?

• Since the officers are all different then you should automatically know that you are going to be using permutation because the order is important.
• 13 is going to be n and 4 is going to be r.
  
• 13P4 = 17,160

example 2: In how many ways can a 20 person student council choose a two person governing council?

• Since the two person governing council can be anyone, then the order isn't important which means you are going to be using combination
• 20 is going to be n and 2 is going to be r
• 20Cr = 190

and that is how you work problems using combination and permutation. I told you is was easy. well thats it for this week. byeeee

--halie

• 
  

Combination and Permutation

Soo, this week we are going to go over some stuff about combination and permutation. You will normally have to use this stuff in word problems when trying to figure out different ways to do stuff.

Permutation is used when you need to find out how many different ways something can be ordered when order is important! The formula for Permutation is:

• nPr = n!/(n-r)!

Combination is used when you need to find out how many different ways something can be ordered when order is NOT important! The formula for Combination is:

• nCr = n!/(n-r)!r!

Now i'm going to work a problem using each.

Example 1. In how many ways can a club with 20 members choose a president and a vice president?

1. Because vice president and president are two different things, order IS important.
2. Use the Permutation formula to solve this problem.
3. 20!/(20-2)!
4. 4Your answer would be 380.

Example 2. In how many ways can the same club as above choose a two person governing council?

1. Because it is not a specific governing council, order is NOT important.
2. Use the Combination formula to solve this problem.
3. 20!/(20-2)!r!
4. Your answer would be 190.

That's about it for now,

Carleyyy(:

Permutation and Combination

Permutation and Combination is section 15-3. We use Permutation when something is important. We use Combination when something is not important.

Formulas:

• Permutation: nPr = n!/(n-r)!
• Combination: nCr = n!/(n-r)!r!

Example 1: In how many ways can a team with 10 members choose 3 different captains?

• Since it says different in the question, we know that it is important. We will use permutation.
• nPr = n!/(n-r)!
• 10P3 = 10!/(10-3)! = 10!/7! = 10 x 9 x 8 = 720

Example 2: In how many ways can you choose 4 marbles from a bag of 20 marbles if the color does not matter?

• Since the question says "does not matter", we know that we should use combination.
• Formula: nCr = n!/(n-r)!r!
• 20C4 = 20!/(20-4)!4! = 20!/16!4! = 20 x 19 x 18 x 17/4 x 3 x 2 x 1 = 116280/24 = 4845

That is it for this section.

-Amber :)

15-3

Permutations and Combinations
This week I'm going to reteach section 15-3, Permutations and Combinations. In certain situations, the order in which choices are made is important, and other times it is not. When the order is important we use the Permutation formula, and when it is not we use the Combination formula.
-Permutation formula: nPr = n!/(n-r)!
-Combination formula: nCr = n!/(n-r)!r!

Example 1: In how many ways can a club with 13 members choose 4 different officers?
-We will use Permuation because the order matters here.
13P4 = 13!/(13-4)! = 13!/9! = 13 x 12 x 11 x 10 = 17, 160

Example 2: In how many ways can you choose 3 letters from the word LOGARITHM if the order of letters is unimportant?
-We will use Combination because the problem clearly states that the order is unimportant.
9C3 = 9!/(9-3)!3! = 9!/(6)!3! = 9 x 8 x 7/3 x 2 = 84

Venn Diagrams babay

This week we learned about Venn diagrams. The concept is one of the simplest things we have learned this year. You need to remember several formulas for each diagram. I will be going over six of them.

First of all, an upside down U means intersection.

A right side up U means union

A letter with a line over it means compliment.

When drawing your diagram, it is helpful to put the total number beneath it. DO NOT PUT THIS NUMBER INSIDE. Make sure to put a U in the top left corner of the diagram.

EXAMPLE



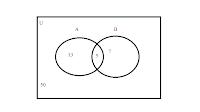
a) (A η B)=5
This means the intersection of A and B which is the middle part of the diagram.

b) (A U B)=25
This means the union of A and B which is everything in the diagram.

c) Ā=57
This is everything that does not have A in it. Therefore it is B and the surrounding area or “neithers”.

d) A=18
This simply means all A. You add what is JUST A and the middle since it is made up of A and B.

e) B=12
All things B therefore just B and the middle section.

f) Ḃ (pretend it’s a line and not a dot)=63
This would be everything that isn’t B therefore A and the surrounding area.

These would be six basic problems relating to Venn diagrams.

--Sarah(:

Venn Diagrams!

Today I'll be teaching you how to make and work venn diagrams. Some things you should know:

• 
  
  The letter n stands for the intersection of the two cSircles.


• 
  
  The letter u stands for the union. The union is both of the circles.


• 
  
  If you have a line over a letter it means that it is a complement, meaning you want everything but the underlined area.
  

Example: There are a total of 40 juniors at East Island High. Ten juniors said they like math. Fifteen junior like science better. Six juniors like both. Find (M u S), (M n S), and the compliment of S.

1. (M u S) means that you want the union of the cicrles. All you have to do simply add.

(M u S) = 31

2. (M n S) means that you're only looking for the intersection of the two circles, which is the middle.

(M n S) = 6

3. Compliment of S means that you're counting everything but S.

compliment of S = 40 - 15 = 35

Woohoo! We're doneee! kbyeee.(:

Venn Diagrams

How to setup a Venn diagram!

All right all you have to do is draw a rectangle and but the little "U" lookin' thing (I don't know how skilled you are as a U writer)  on the top left of the inside of the rectangle; then write the total amount on the outside of the rectangle, no it doesn't matter where you place the number for all you OCD people out there. Now draw the two circles in the center of the rectangle in which there is a large enough space in which they intersect to write a number. Write one total of group A on the left circle and the total of group B on the left circle and where ever they happen to over-lap in the middle, intersection. Write the remainder on the bottom left of the rectangle.

Congratulations... you can now cross one thing off of your laborious bucket list!!!! -__-

~ Parrish Masters Jr.

15-1 venn diagrams

today is learning about how to do and make venn diagrams. its is really simple just have to know wht you are doing. first thing is to know about the union, intersection, and if the equation has a compliment. the symbol for a union is "u" and symbol for an intersection is "n". a compliment will have a line over your variable. with an intersection all you are looking for is whats in the middle of the wo circles. the union is both circles and the intersection but you only count the intersection one time. so lets do an example to make this more clear.




EX: a small college has 1000 students. F= college freshman, and M= set of music majors. tell the number of members each question asks for.

here is your venn diagram.

1) F n M
this is means find the intersection of F and M which = 15

2)F u M
this means find union of F and M..add all 3 numbers which = 350

3) compliment of F
this means find everything but F including the total 1000 freshman which is 1000-300= 700

4) compliment of M
this means find everything but M including the total 1000 freshman which is 1000-65=935

15-1 Venn Diagrams

Things you should know:

• The letter n stands for the intersection of the two circles.
• The letter u stands for the union which is both of the circles.
• When there is a line over a letter that means it is a complement. This simply means that you want everything that is not under the line.
• Formula: n(A u B)=n(A)+n(B)-n(A n B). <------ It only tells you to not count the middle number of the circles twice.

Example 1: Find (A n B), (A u B), and the complement of A. A has 80 (first circle), B has 40 (second circle), intersection has 10, left over is 360, and the overall number is 890.

• (A n B) simply means what is in the middle. So (A n B) = 10.
• (A u B) simply means what does both of the circles (including the middle) add up to. So (A u B) = 130.
• The complement of A simply means everything except for A. So the complement of A = 400.

Amber :)

15-1

Venn Diagrams

This week I'm going to reteach lesson 15-1, Venn Diagrams. In this lesson, we learned how to work problems dealing with intersections, unions, and compliments. An intersection(n) is the middle of two joined circles. A union (u) is everything within two joined circles. A compliment is represented by a line over a letter, and is everything but the amount under that letter.

*I couldn't upload a picture, so I'm going to do my best on this example without one.

Example 1: There are 1,000 total students at Oakville High. S(Students who just play sports) has 320. M(Students who just take Math) has 70. 30 students do both. 580 students don't do either. Find a) (SuM), b) (SnM), c) compliment of S, d) compliment of M, and e) compliment of (SuM)

• a) (SuM) is the union, so that would be all of the students counted inside the intersected circles. Therefore, (SuM)=420.
• b) (SnM) is the intersection, so that is the students who do both sports and Math. Therefore, (SnM)=30.
• c) The compliment of S would be all of the students who are not playing sports. So, the compliment of S=650.
• d) The compliment of M would be all of the students not taking math, so that would =900.
• e) The compliment of (SuM) would be all of the students not doing either activities. So the compliment of (SuM) = 580.

venn diagrams

ok so this week im going to talk about the venn diagrams. The first thing you need to know is a few things about the veen diagrams and how they work. Here are a few things you must know.

The intersection= n (which is the middle of the two circles)

The union=u (which is all of the two circles)

The complement is when there is a line over the letter. This means you want all elements that are not whatever is under the line.

You might also need to know this formula: n(A u B)=n(a) + n(b) - n(A n B)

That formula is so you don't count the middle number twice. ^^^^^

Ok soo i dont feel like drawing this diagram so im going to explain it so follow closely.

Theres a total of 20.
The first circle is B and it has 5
The second circle is O and it has 5.
The middle has 10.
And there is 0 leftover.

*(B n J)= 10
*(B u J)= 20
*complement of B which is 5.

Ohhhhhh Yeaaaaaaa all done. peace playas

Counting Principle

This weekend I am going to teach you all about the counting principle. These problems are very easy after you figure out what you have to do. Different problems have different methods of solving them. Some problems may be simple multiplication while some may require you to raise to a power and then multiply. Now I will show you some examples of these problems.

Example 1: How many ways can 6 students stand in line?
First of all you would draw six little lines for each spot in line. Then you would write one number in each spot. It would look like this 6 5 4 3 2 1. Then you would multiply all of the numbers together. The answer would be 720.

Example 2: In how many different ways can you answer 6 multiple choice questions if each question has two answer options?
For this problem you would take the number of answers, 2, and raise it to the number of questions, 6. 2^6=64. The answer would be 64.


-Braxton-

The Counting Principle

The Counting Principle can be difficult if one doesn't understand what the particular problem is asking for. Once that's figured out, it's really simple. Sometimes the problem asks for order, other times it can be random. Those all affect how the solution will come out to be so that has to be checked.

Example 1: Ice cream can come in both a cup or a cone. The flavors available are vanilla, chocolate, and strawberry. How many possible outcomes are there? (Assume that each person is receiving only a scoop of ice cream)

To determine: all one needs to do is multiply the two containers of how the ice cream is served by the flavors of every ice cream to get the answer

#: 2x3= 6

Example 2: I have 3 shirts and 4 pants. How many different outfits can i have?

Multiply 3x4=12 different outfits.

Oh what fun it is to blog!

So, today we're going to learn about the counting principle. It's really easy if you think about it. I'm going to go straight into examples because it's easier to see that way.

Example 1. How many ways can 5 people stand in a line?

First thing you should do is draw 5 little dashes and put how many people could be in that spot. So it would be 5 4 3 2 1. Now you have to multiply them together. This is also the same thing as saying 5!. You answer would be 120.

Example 2. How many ways can you answer 5 true false questions?

This one is a little bit different. Since you can have either true or false you would do that number raised to how many questions there is. So you would get 2^5 which is 32. 32 I your answer

Example 3. How many sweater/pants combinations can you have with 2 pants and 4 sweaters?

On this problem all you have to do is multiply the two number together. So you answer is 8.

That's about it for counting principle.

--Carley

15-1 Venn Diagrams

So I guess this week, I'll teach you how to work problems using venn diagrams. They are really easy. The good thing about this week is that venn diagrams don't have that many notes. So I guess I should get started.

First, there are a few things you need to know:

1. The intersection= n (which is the middle of the two circles)
2. The union=u (which is all of the two circles)
3. The complement is when there is a line over the letter. This means you want all elements that are not whatever is under the line.
4. You might also need to know this formula: n(A u B)=n(a) + n(b) - n(A n B)
5. That formula is so you don't count the middle number twice. It is very important that you don't count the middle twice! So don't forget that!

Okay, so now I am going to work an example. WOOO!

Example 1: Given the diagram below find (F n M), (F u M), and the complement of F.

Okay, well it isn't letting me download a picture on hereee. So I am just going to have to explain what it looks like.

1. The first circle is F and it has 285.
2. The other circle is M and it has 50.
3. The middle of the two circle is 15.
4. The left over is 650.
5. The overall number of the diagram is 1000.

• (F n M)= 15. Remember that when it is n it is always what's in the middle.
• (F u M)= 350. Thats all the circles added up, including the middle.
• The complement of F is everything except for F, which is 700.

Well, that's it for this weeek. BYEE :)

--Halie

inverses

today im teaching you how to find inverses. there is a couple of rules though. the first rule is that to have an inverse that is a fumction it has to cross the horizontal line test. to find the inverses all you are going to do is switch the x's and the y's and solve for y. to prove something is an inverse do (f o *inverse of* f) (x) and (*inverse of* f o f) and both should equal x. so below i will provide an example.


EX:
state whether the function f has an invers. if f^-1 exists then find a rule to prove it.

f(x)= 3x - 5
first switch x and y
x=3y - 5
solve for y
y= x + 5 / 3
now prove it
(f o f^-1)= f(x)= 3(x+5 / 3) -5
3's cancel leaving you with x+5 - 5 which = x
(f^-1 o f)= f^-1(x)= (3x - 5) +5 / 3
3's cancel 5's cancel leaving you with x
these are inverses

Function Notation

This weeks blog will be about Function Notation! YAY!!

Formulas:

(f+g)(x) = Add equations

(f-g)(x) = Subtract equations

(f x g)(x) = Multiply equations

(f/g)(x) = Divide Equations

Examples

f(x)= x + 3 g(x)= x + 3

Find (f + g)(x)

(x + 3) + (x + 3)=

2x + 6!!!

Yay for blogs

4-3

Chapter four is about a lot of different things. The test on these things is Tuesday. Great. Anyway this week my blog will be on symmetry.
To check for symmetry:

1. About the x-axis
a. Put a negative in front of y and simplify. The new equation is symm. About the x-axis.
b. If it matches the original it is symmetric about the x-axis.

2. About the y-axis
a. Plug in a (-x). The new equation is symm. About the y-axis.
b. If it matches the original it is symmetric about the y-axis.

3. About the origin
a. Plug in a (-x) and put a negative in front of y. The new equation is symm. about the origin.
b. If it matches the original it is symmetric about the origin.

4. About y=x
a. Switch the x and y and solve for y. The new equation is symm. about y=x.
b. If it matches the original it is symmetric about y=x

EXAMPLE
Is y=x^2+9 symmetric about I) the x-axis, II) the y-axis, III) the origin, IV) y=x

I. –y=x^2+9 In this equation you can reverse the signs.
Y=-x^2-9 Since the equations do not match, it is not symm about the x axis.

II. y=(-x)^2+9 Since the negative is inside (), it will stay negative.
y= -x^2+9 The equations do not match therefore it is not symm about the y axis.

III. -y= (-x)^2+9 Reverse the signs.
y= x^2-9 Not sym about origin.

IV. x=y^2+9 Since it is impossible to change this back to x^2, you automatically know that it is not symmetric about y=x.

Good luck guys. Oh and since B-Rob is in California does that mean this has to be posted by midnight her time or our time? o_O

--Sarah

Chapter 10

Chapter 10

Chapter 10 is strictly formulas. It may not be easy to memorize all of them, but once you do this will be an extremely easy chapter. You will also need the trig chart again in this chapter! Today I'm going to explain section 10-1's formulas.

They are:

1. cos(alpha+/-beta)=cos alpha cos beta-/+sin alpha sin beta

2. sin (alpha+/-beta)=sin alpha cos beta+/-cos alpha sin beta

3. sin x+sin y=2sinx+y/2 cos x-y/2

4. sin x-sin y=2cosx+y/c sin x-y/2

5. cos x+cos y=2cosx+y/2cosx-y/2

6. cos x-cos y=-2sinx+y/2 sin x-y/2

Now for an example.(REMEMBER: in this chapter you REPLACE, NOT PLUG IN!)

Find the exact value of Sin 15
1. Since sin 15 isn't on the trig chart, you must use a formula that will make it.
2. So you will use Sin(45-30)
3. You will now get, Sin45 cos 30-cos 45 sin30
4. Using the trig chart, you get Sqrt 2/2 x sqrt 3/2 - Sqrt 2/2 x sin 1/2
5. Simplify. You get (sqrt 6-sqrt 2)/4

That's how you do thattt :)

Carleyyy :)

Chapter 4

To find your answers for symmetry, follow the steps below

a/b the x-axis

First, place a negative sign in front of all the y's and simplify

Second, check to see If the equation when simplified is like the original equation then it is symmetrical about the x-axis

Third, if not symmetrical it has to be NOTED that it is not symmetrical about the x-axis.

a/b the y-axis

First, plug in (-x)

Second, check to see if the equation when simplified is like the original equation then it is symmetrical about the y-axis

Third, if not symmetrical it has to be NOTED that it is not symmetrical about the y-axis

a/b the origin
First, plug in (-x) and place a negative sign in front of all the y's
Second, check to see if the equation when simplified is like the original equation then it is symmetrical about the origin
Third, if not symmetrical it has to be NOTED that it is not symmetrical about the origin

y=x
First, switch the x's and y's and solve for y
Second, check to see if the equation when simplified is like the original equation then it shows that y=x

Third, if not, it has to be NOTED y doesn't equal x.

Example: x^2+xy=4

i. x^2+x(-y)=4

not symm. a/b the x-axis

ii. -x^2+-xy=4

not symm. a/b the y-axis

iii. -x^2+-x-y=4

not symm. a/b the origin

iv. y^2+yx=4

y doesn't equal x no

4-3 Symmetry

This weekend I am going to teach you all how to check to see if a graph is symmetrical about the x axis, y axis, the line y = x, and the origin. These problems are fairly simple but there are some things that you need to know before you begin.

Notes:

About the x-axis
• First you put a negative in front of the y and simplify
• The new equation is symmetrical about the x-axis
• If the simplified equation matches the original equation then it is symmetrical about the x-axis

About the y-axis
• First you have to plug in a (-x)
• The new equation is symmetrical about the y-axis
• If the simplified equation matches the original equation then it is symmetrical about the y-axis

About the origin
• You have to plug in a (-x) and put a negative in front of the y
• The new equation is symmetrical about the origin
• If the simplified equation matches the original equation then it is symmetrical about the origin

About y = x
• You must switch the x and y and solve for y
• The new equation is symmetrical about y = x
• If the simplified equation matches the original equation then it is symmetrical about y = x

Example: xy^2 = 4x – 6
i. x(-y^2)=4x-6 no
ii. (-x)y^2=4(-x)-6 -xy^2=4(-x)-6 no
iii. (-x)(-y^2)=4(-x)-6 xy^2=4(-x)-6 no
iv. yx^2=4y-6 no

Function Notation

Formulas:
(f+g)(x) = Add equations
(f-g)(x) = Subtract equations
(f x g)(x) = Multiply equations (in writing the "x" would be a closed circle)
(f/g)(x) = Divide Equations

Examples:
f(x) = x + 83, g(x) = x + 3 ....... Find (f-g)(x) (Replaces the x's in the other equation with what the equation is = to... this makes sense in my mind)
(f-g)(x) = x+83-3
=x+80 (Yellow highlight = answer)


Find (f+g)(x)
(F-g)(x) = x+83+3
= x+86

Symmetry

This section is on symmetry. There are four places you can check for symmetry: the x-axis, the y-axis, the origin, and the line y=x.

Things you need to know are as follows:

I. X-axis

• Put a negative in front of the y's and simplify.
  
• It is symmetric about the x-axis if it matches the original problem.

II. Y-axis:

• Put a (-) in front of the x's.
  
• It is symmetric about the y-axis if it matches the original problem.

III. Origin:

• Put a (-) in front of the x's and a negative in front of the y's.
• It is symmetric about the origin if it matches the original problem.

IV. Y=x

• Switch the x and y.
• Solve for y.
• It is symmetric about the line y=x if it matches the original problem.

Example 1: y=x^2 - 8

I. -y=x^2 - 8. y=-x^2 + 8. Since the new equation is not the same as the original: not symmetric about the x-axis.

II. y=(-x^2) - 8. y=x^2 - 8. Since the new equation is the same as the original: symmetric about the y-axis.

III. -y=(-x^2) - 8. -y=x^2 - 8. y=-x^2 + 8. Since the new equation is not the same as the original: not symmetric about the origin.

IV. x=y^2 -8. y= square root of x + 8. Since the new equation is not the same as the original: not symmetric about the line y=x.

Amber :)

Symmetry

Today I'll be teaching how to check for symmetry. You can check for symmetry about the x-axis, y-axis, the origin, and line y=x.

To check for symmetry about the x-axis you must:

• put a (-) in front of the y's and simplify.


• if it matches the original problem then it is symmetry about the x-axis

To check for symmetry about the y-axis you must:

• plugin a (-) in front of the x's and simplify


• if it matches the original problem then it is symmetry about the y-axis

To check for symmetry about the origin you must:

• plugin a (-) in front of the x's and y's then simplify


• if it matches the original equation then it is symmetry about the origin

To check for symmetry about line y=x you must:

• switch the x's with the y's and solve for y


• if it matches the original equation then it is symmetry about line y=x

Example 1: y^2+xy=5

i. (-y)^2+x-y=5

-y^2-xy=5

no

ii. y^2+-xy=5

y^2-xy=5

no

iii. -y^2-x-y=5

-y^2+xy=5

no

iv. x^2+yx=5

no

4-3 Symmetry

So this week I am going to explain how to work problems that make you check for symmetry. These problems have a lot of notes, but are very easy to do. So here are the notes that you are going to need to know:

About the x-axis:

• Put a negative in front of the y and simplify.
• The new equation is symmetry about the x-axis.
• If it matches the original it is symmetry about the x-axis

About the y-axis:

• Put a negative in front of the x's
• The new equation is symmetry about the y-axis
• If it matches the original it is symmetry about the y-axis

About the origin:

• Put negative in front of the x's and y's
• The new equation is symmetry about the origin
• If it matches the original it is symmetry about the origin

About y=x

• Switch the x and the y and solve for y.
• The new equation is symmetry about y=x
• If it matches the original it is symmetry about y=x

So now I am going to work an example to help you to better understand what you are doing in problems like these.

Example 1: y^2-xy=2

1. -y^2-x(-y)=2
2. -y^2+xy=2
3. Not sym about x-axis

1. y^2-(-x)y=2
2. y^2+xy=2
3. Not sym about y-axis

1. -y^2-(-x)(-y)=2
2. -y^2-xy=2
3. Not sym about origin

1. x^2-yx=2
2. Not sym about y=x

And it is as easy as that. Well that is it for this weeek. BYEE

--Halie :)

Symmetry

4-3 Symmetry

In this lesson we learned how to check for symmetry about the x-axis, y-axis, origin, and line y=x.

To check for symmetry...

1) About the x-axis:

a) Put a negative in front of y, and simplify.

b) If the new equation matches the original, it is symmetric about the x-axis.

2) About the y-axis:

a) Plug in a (-x).

b) " "

3) About the origin:

a) Plug in a (-x), and put a negative in front of y.

b) " "

4) About y=x:

a) Switch the x and y, and solve for y.

b) " "

Example 1: Is y^2 + xy = 5 symmetric about i. the x-axis, ii. the y-axis, iii. the origin, iv. the line y=x?

i. -y^2 + x - y = 5 = y^2 -xy = -5 --> not symmetric about the x-axis

ii. y^2 (-x)y = 5 = y^2 - xy = 5 --> not symmetric about the y-axis

iii. -y^2 + (-x) -y = 5 = -y^2 + xy = 5 --> not symmetric about the origin

iv. x^2 + yx = 5 --> not symmetric about the line y=x

Example 2: " " y = x^2 +4

i. -y= x^2 + 4 = y= -x^2 - 4 --> not symmetric about the x-axis

ii. y= (-x)^2 + 4 = y= x^2 + 4 --> symmetric about the y-axis

iii. -y= (-x)^2 + 4 = -y= x^2 + 4 = y= -x^2 -4 --> not symmetric about the origin

iv. x= y^2 + 4 = y^2= x - 4 = x= sq. root of x-4 --> not symmetric about the line y=x

chapter 4

This week we started Chapter Four. This chapter has to do with domain and range. Anyway, here we go with the blogging and the learning and what not. I will be going over finding the domain and range of a polynomial.

-Domain: the interval of x values where the graph exists.

-Range: the interval of y values where the graph exists

-Zeros, x-int, root- set=0 solve for x

-To be a function the graph must pass the vertical line test.

-If given points the domain is the list of all x-values and range is a list of all y-values in { }

To find domain and range:

Polynomials

Domain: (-infinity, infinity) ALWAYS

Range: odd (-infinity, infinity) always x^2 (-b/2a, infinity) if parabola opens up or (-infinity, -b/2a) if parabola opens down.

Example:

Find the domain and range of the following
F(x)=7x^3+4x^2-18

As previously stated, the domain of a polynomial is always (-infinity, infinity)

Since the largest exponent is odd, the range is (-infinity, infinity).

Example 2:

Find the domain and range of the following
F(x)=7x^2-28

The domain is (-infinity, infinity)

The parabola opens upwards therefore the range will be (-b/2a,infinity).

The range is [2, infinity)

Good luck on the test everyone (:
--Sarah

function notation!!!

The first thing we are going to do is learn a few formulas that you will need for this section. As you can tell alomst every section in math contains formulas. Can you imagine how hard math would be if they didnt have formulas to help us with these wonderful problems?!?!?! Its crazy if you sit here and start thinking about how many formulas we have went through so far this year and we are only halfway through! Wow thats at lot!!! Anyway here are the formulas:

(f+g)(x) >you add the equations!

(f-g)(x) > you subtract the equations!

(ftimesg)(x) > you multiply the equations!

(f/g)(x) > you divide the equations!

So now that i have showed you the formulas you will now see an example or two of how to apply these formulas to everyday life!

f(x)= 8 g(x)=2 find (f+g)(x)
8+2
=10

BAM!!!!!!

Holiday Blog # 2 Multiplying Matrices

There are two or actually three ways to multiply matrices if you include the use of a calculator. One being multiplying rows and columns, two being the way it's shown in the notes, and three being simply the use of a calculator.

To multiply matrices in a ti-84 calculator, first go to 2nd then press x^-1 then arrow to the right to edit and then press enter. Enter the dimensions of the first matrix and then enter the inner numbers.
After that is done press 2nd then mode and repeat the previous steps for the second matrix.
Now press 2nd then x^-1 then press enter. Press the multiplication symbol and then press 2nd then x^-1 move down to matrix B and then press enter and enter once more to get the product.

- Parrish Masters

Function Notation

Hello Everybody. Now i am going to teach you about function notation.

First lets get the formulas:

(f + g)(x)= add equations

(f - g)(x)= subtract eqns

(f *g)(x)= multiply (closed circle)

(f/g)(x)= divide

(f o g)(x) or f(g(x))= replace all x's in the f(x) eqn w/ the eqn g(x)

Now lets do a few examples so you can get the hang of it. YAYYYYYYYY

ex 1: f(x)= x + 4 g(x)= x + 2. Find the rule for (f + g)(x)

you simply just add the equations

(x + 4) + (x + 2)= 2x+6

ex 2 " "

Function Notation

Today I am going to explain how to work function noatation problems. Function notations are mainly algebra, which makes it really easy. There are some formulas that you need for these and they are as follows:

• 
  
  (f+g)(x) - This means that you add the f(x) equation and the g(x) equations together


• 
  
  (f-g)(x) - This means that you subtract the g(x) equation from the f(x) equation


• 
  
  (f o g) - This means that you multiply the f(x) equation and the g(x) equation


• 
  
  (f/g) - This means that you divide the f(x) equation by the g(x) equation

Remember, if there a number instead of (x) replace that x with the number given.

Example 1: f(x) = x+1 g(x) = x^2-1, Find the rule for (f+g)(x)

1.You are going to add the f(x) and the g(x)

(x+1)+(x^2-1)

2. You have to factor within the equations if possible. If not possible, then cancel anything if possible.

Since there is nothing to factor, we skip to the cancelling step. +1 and - 1 can be cancelled.

x^2+x

3. Now you have to factor if posisble.

x(x+1)

Your answer is x(x+1) .

Function Notation

Typically, these problems are given in the two forms of f(x) and g(x) equations. These problems are really easy to solve. The hardest part is remembering which equation to use.

Rules:
(f + g) (x) - add equations
(f - g) (x) - subtract equations.
(f * g) (x) - multiply equations.
(f / g) (x) - divide equations.
(f o g) (x) - replace all x's in the f(x) equation with the equation g(x)
if there is a number then you use the number instead of x

Example: f(x) = x^2 + 2x and g(x) = x+4
(f+g) (x) <-----------------------------Determine which equation you are going to use
(x^2 + 2x) + (x+4) <------------------- Plug in the f(x) and g(x) equations into it

x^2 + 3x + 4 <------------------------- Add as follows
(x + 4) (x - 1)<------------------------- Factor for your final answers

Function Notation

This weekend I am going to teach you all how to work function notation problems. These problems are worked by using algebra. There are some notes that you need to know before I show you all an example of a function notation problem.

Notes:
• (f + g) (x)  This means that you have to add the f (x) equation and the g (x) equation.
• (f – g) (x)  This means that you have to subtract the f (x) equation and the g (x) equation.
• (f * g) (x)  This means that you have to multiply the f (x) equation and the g (x) equation.
• (f/g) (x)  This means that you have to divide the f (x) equation and the g (x) equation.
• (f o g) (x)  This means that you replace the x’s in the f equation with the g equation.
• If there is a number instead of an x, just plug that number into the equation.

Example: f (x) = x + 3 g (x) = x – 2
Find (f + g) (x)
• (x + 3) + (x – 2)
• x + 3 + x – 2
• 2x + 1

-Braxton

Function Notation

This week I am going to explain how to work function notation problems. Which is very easy. All your really doing is basic algebra, which you should already know. So before I work some examples, you are going to need a few notes.

NOTES:

• (f+g)(x) means to add the f(x) equation and the g(x) equation.
• (f-g)(x) means to subtract the f(x) equation and the g(x) equation.
• (fxg)(x) means to multiple the two equations together.
• (f/g)(x) means to divide the two equations.
• (fºg)(x) or f(g(x)) means to replace all the x's in f(x) with g(x)
• If x is replaced with a number, plug into the equation.

Okay, so you are going to use those formulas to work the problems I am about to show you. SO here are some easy examples:

EXAMPLE 1: Using this equation f(x)=2x+1 and g(x)=x-4 find: (f+g)(2)

• You are going to replace all the x's with 2.
• 2(2)+1 + 2-4
• Once you do that, all you have to do is just solve the problem.
• So your answer is going to be 3.

EXAMPLE 2: Using this equation f(x)=x^2+x and g(x)=x+1 find: (f+g)(x)

• Since they don't give you any number to replace the x's for you are just going to work the problem as far as you can. But DO NOT solve for x. That isn't going to be your answer.
• x^2+x + x+1
• Once you have that as your problem you are going to factor.
• Once you factor you are going to get (x+1)(x+1) which is going to be your answer.

And that is how you work function notation problems! WOOHOO.

--Halie

Ch. 4 Section 1

Fraction: Fractions do not have a range... <- Remember this

Domain is found through factoring the top/bottom, then canceling if at all possible, set x= # that is canceled on the side, then set the bottom equal to zero and then solve for x, then write your answer in interval notation stopping at the numbers found in steps two and three.

Example.)  x^2 + 1 / (x-1) (x+2), Factor/Cancel: (x+1)(x-1) / (x-1) (x+2),             x=1
x+2 = 0                                                                                                                     x=2
Domain: (-infinity,1)u(1,2)u(2,-infinity)

- Parrish Masters

Domain and Range

This is Chapter 4: Section 1.

This you should know:

• Domain-the interval of x values where the graph exists.
• Range-the interval of y values where the graph exists.
• Zeroes-x intercept, root-set equal to zero, and solve for x.
• A graph must pass the vertical line test in order to be a function.
• If you are given points, the domain will be the list of all x-values and range will be the list of all y values. It will be in { }.

How to find domain and range for polynomials and absolute values:

• Polynomials: Domain will always be (-infinity, infinity). Range- (-infinity, infinity), if it is x^2-(-b/2a, infinity) or (-infinity, -b/2a).
• Absolute values: Domain-(-infinity, infinity). Range-[0+a, infinity) or (-infinity, 0+a] if a is positive, [0-a, infinity) or (-infinity, 0-a] if a is negative.

Example 1: Find the domain and range of the following: f(x)=7x^3+4x^2+x-9

• Domain=(-infinity, infinity)
• Range=(-infinity, infinity)

Example 2: Find the domain and range of the following: f(x)=-5x^2+8x-10

• Domain=(-infinity, infinity)
• Range=(-infinity, -8/2(-5))=(-infinity, -8/-10)=(-infinity, 4/5)

Example 3: Find the domain and range of the following: y=|x-6|+2

• Domain= (-infinity, infinity)
• Range=[2, infinity)

Amber :)

Domain and Range

Chapter 4, Section 1: Domain and Range
In this lesson, we learned how to find the domain and range of graphs, the zeroes, and how to determine if its a function or not.
To find the..
-domain: the interval of x values where the graph exists
-range: the interval of y values where the graph exists
-zeroes: x intercept, root- set equal to 0, solve for x
-For the graph to be a function, it must pass the vertical line test.
*If you're given points, the domain will be the list of all x values, and the range will be the list of all y values in { }.

Here's how to find the domain and range of polynomials(very simple!):
The domain is always: (-infinity, infinity). The range is always (-infinity, infinity).

Example 1: Find the domain and range of the following: f(x) = 4x^3 + 2x^2 + 6x - 12
-Domain: (-Infinity, infinity)
-Range: (-infinity, infinity)

Example 2: Find the domain and range of the following: f(x) = -3x^2 +4x - 6
-Domain: (-infinity, infinity)
-Range: (-infinity, -4/2(-3)) = (-infinity, 2/3)

function notation

so this week we learned about how to do function notation. function notation is a really easy process if you can just pay attention on what to do. usually you will be given an f(x) and a g(x) and from there you will determine which rule you will use. i will give the rules below in just a minute. your final answer should be factored out if you have to solve with (x) or a number if you solve with a (#). here are the rules then an example.


Rules:
(f + g) (x) - add equations
(f - g) (x) - subtract eqs.
(f * g) (x) - multiply eqs.
(f / g) (x) - divide eqs.
(f o g) (x) - replace all x's in the f(x) equation with the equation g(x)
if there is a number then you use number instead of x

EX: f(x) = x^2 + x  g(x) = x+1
(f+g) (x)
first just plug in for f and g
(x^2 + x) + (x+1)
then add as followed
x^2 + 2x + 1
factor for final ans
(x + 1) (x + 1)

Function Notation

This week we are going to learn about function notation. It's really easy. All you have to do is basic algebra as long as you know what each thing is asking for. With that being said i'm going to show you exactly what each problem is asking you to do!

• (f+g)(x) means to add the f(x) equation and the g(x) equation.
• (f-g)(x) means to subtract the f(x) equation and the g(x) equation.
• (fxg)(x) means to multiple the two equations together.
• (f/g)(x) means to divide the two equations.
• (fºg)(x) or f(g(x)) means to replace all the x's in f(x) with g(x)
• If x is replaced with a number, plug into the equation.

Example 1:

Using the equations f(x)=2x+1 and g(x)=x-4 find:

a) (f+g)(2)

• (2(2)+1)+((2)-4)
• =3

b) f(g(1))

• (1)-4
• =-3
• 2(-3)+1
• =-5

That's about it for now on function notation! Have a great day or not, THE CHOICE IS YOURS! :)

--Carley :)

Degrees to Radians and Vise Versa

Holiday Blog Uno...


Degrees - Radians:
To convert to degrees to radians, all you do is divide a number by 180 and add the pie symbol behind the number; so if you wanted to convert 360 to radians, you'd divide 360 by 180 and get 2pie.

Radians - Degrees:
To convert from radians to degrees you do the opposite, basically multiply by 180 and leave out the pie symbol.
2pie times 180 = 360

And one more blog about old stuff

Let me show you how to find all six trig functions from a triangle.

All you need to know is the formulas for all the trig functions.

They are: sin=y/r csc=r/y
cos=x/r sec=r/x
tan=y/x cot=x/y
Example:

Imagine you have triangle ABC where AB=6 BC=3 CA=2, Find all six trig functions.

For this problem, were going to call AB the radius, BC will be on the x values, and CA will be the y's since i cant find a triangle like the one im picturing.

Now its just a matter of plugging into all the formulas.

The final answers will be: sin=1/3 csc=3
cos=1/2 sec=2
tan=2/3 cot=3/2
I know this was a terrible example of trying to esrcibe a triangle but its all i can do.
YAY FOR BLOGS!!

Old Stuff Again

Its getting late so lets make this quick and lets talk about reference angles.

Steps: 1 find the original quadrant and sketch it.

2 positive or negative.

3 either subtract 360 or 180 until the angle is in between 0 and 90.

Example: Find the reference angle for sin 600

600-360=240 so now you know the original quadrant is 3

Sin is positive in Q3

240-180=60

Now we can know that the reference angle is sin60

Old Stuff

My stupid self left my binder at school for the christmas break so i have to do these blogs on the simplest things i can remember.

Lets talk about the conversion of radians to degrees and degrees to radians

Degrees to Radians
Formula: Degree x pi/180

Note: When you put this in your calculato, leave out pi and just put it in the fraction at the end.

Example: Convert 45degrees to radians

45 x pi/180

45/180= 1/4

pi/4

Radians to Degrees
Formula: radians x 180/pi

Example: convert pi/3 to degrees

pi/3 x 180/pi

the pi's cancel and you get 180/3

The final answer is 60 degrees.

YAY FOR BLOGS!!!

MERRY CHRISTMAS AND A HAPPY NEW YEAR!!

Hello B-Rob and the rest of class. If you guys didnt know, the basketball team was out of town for both weeks of Christmas vacation. I was in town for Christmas Eve and Christmas, and from this past Sunday to now. I didnt have much of a Christmas break and was out of town for the weekends. SO i know this is a little late but i am going to do all 3 of my blogs right now. Please dont take off any points. Thanks;)

P.S. Merry Christmas and Happy New Year to everyone. I hope Santa was good to everybody

8-4

today i will show you relationships amoung functions. some key facts about this is sin x/ cos x = tanx and cos x / sin x = cot x. the steps to follow loosely meaning not exactly is do algebra first then identities- try pythagorean theorm then move everything into sin and cos if its helps, then algebra again. here is an example to see how it works.


EX: csc x - cos x (cot x)
1/sin x - cos x/1 (cos x/sin x)
1/sin x - cos^2 x/sin x
1-cos^2/sin
sin^2/sin x
=sin x

degrees and radians and new years and stuff

Today we are going to convert degrees to radians and then radians to degrees. Pay close attention because this is VERY important in trig.

You are going to multiply 60 by pi/180.

All you really have to do is simplify 60/180 then add pi in.

You’re answer should therefore be 1pi/3, which is simply pi/3

Now for radians to degrees.

Convert 5pi/4 to degrees.

To convert radians to degrees the process is almost exactly the same

You multiply 5pi/4 times 180/pi.

The pi cancels leaving you with 5/4 times 180.

5 X 180= 900/4=225 degrees.

If you do not get a whole number, you need to convert to degrees minutes and seconds.

To convert to degrees minutes and seconds you multiply the number behind the decimal by 60. This number becomes minutes. If there is another set of numbers behind the decimal, multiply by 60 again. If you still don’t have a whole number after multiplying by sixty twice, you drop the number behind the decimal and the number in front of the decimal becomes seconds.

YOU WILL GET POINTS OFF IF YOU DO NOT CONVERT.

I’m sorry this blog is poorly written but I’m exhausted. HAPPY NEW YEAR :D

See you guys Wednesday :/

--Sarah

10-1 Review

This week I'm going to review the sum and differences of sine and cosine. You will need the trig chart again in this chapter. Today I'm going to explain the sum and difference formulas of sine and cosine.They are:
1. cos(alpha+/-beta)=cos alpha cos beta-/+sin alpha sin beta
2. sin (alpha+/-beta)=sin alpha cos beta+/-cos alpha sin beta
3. sin x+sin y=2sinx+y/2 cos x-y/2
4. sin x-sin y=2cosx+y/c sin x-y/2
5. cos x+cos y=2cosx+y/2cosx-y/2
6. cos x-cos y=-2sinx+y/2 sin x-y/2

Now for an example.(REMEMBER: in this chapter you REPLACE, NOT PLUG IN!)
Find the exact value of Sin 15
1. Since sin 15 isn't on the trig chart, you must use a formula that will make it.
2. So you will use Sin(45-30)
3. You will now get, Sin45 cos 30-cos 45 sin30
4. Using the trig chart, you get Sqrt 2/2 x sqrt 3/2 - Sqrt 2/2 x sin 1/2
5. Simplify. You get (sqrt 6-sqrt 2)/4
And that's all there is to it (:

Matrices

Things you need to know:

• A^t means to switch the rows and columns in the matrix.
• When you are adding matrices, they must be the same dimensions (rows x columns).
• When you are adding matrices, you add the corresponding entries.
• When you are doing multiplication, you multiply every entry by the number.

Example: 1

• What are the dimensions of the matrix? 2x3 (2 rows x 3 columns)
• Find M^t.
• Find 2M.

-Amber :)

Reference angles!!!

Soo today I'm going to talk about how to find reference angles! I don't have my binder so I'm going to wing it. last night was new years eve and I'm not feeling to swell so I'm going to make this a short blog. anyway there is this thing called the unit circle and its in the shape of a circle. It begins on the right side with 0 degrees then goes up to 90 degrees. Next it goes to the left side with 180 degrees then to the bottom with 270 and back to the right at 0 degrees which is also 360 degrees. in order to find a reference angle you can add or subtract 180 but the new angle has to be between 0 and 90. Soo if you got an angle that is 180 you subtract 180 and your new angle is 0 degrees. You can also do it with negative angles. So if you have -120 degrees you add 180 and will end up 60 degrees. You can also do it with radians but my brain isn't up to the job at this time of day.

11-2

Changing from polar to rectangular is quite simple. The most common mistake when performing these problems is forgetting i, the imaginary number which goes at the end of the equation. The formula is as follows:

z=x +yi

Now, in order to get to this form when one is given Acis(theta).

You must first break down A into its respective components which are A cos theta

A sine theta

After you figure that out, you may then place the answers into the rectangular form equation above with the appropiate components for each answer.

Example:

5 cis 75

1. Break it up into its respective components

5 cos 75= 1.294 5 sin 75= 4.830

2. Plug this into your rectangular equation above.

z= 1.294+4.830i

(Don't forget to put the i at the end!)

-Sameer