HAPPY NEW YEAR!

Today, we are going to begin reviewing about simple matrices. We are going to review three things: how to add and subtract, how to multiply, and how to find the dimension of a matrix. When adding and subtracting them, you have to make sure they have the same dimensions. Dimensions are the number of rows by the number of columns. I'm going to show you an example of adding and subtracting matrices.

Example 1.

2 2 + -3 5 = -1 7

4 6 4 -1 8 -5

They next thing we are going to review about matrices is how to multiply them. Multiplying can be a bit more difficult but it still is not that hard. When looking at dimensions of two matrices, this is what it has to look like AxB BxC. Once you know you can multiply, you multiply rows by columns.

Example 2.

2 x 3 -4 = -2

1 -1

I hope this made you remember how to add and multiply simple matrices!

Have a Great New Year!

---Carley!

10-3 Review

This weekend I am going to go over the material that we learned in chapter 10 section 3. These two sections contain the same types of problems as sections 1 and 2. The only difference is that now you are going to use double angle and half angle formulas to solve the trig equations. You need to follow the same steps that you followed in the previous sections of this chapter.

*Always remember to replace, not plug in.

Formulas:
1. sin 2a= (2 sin a) (cos a)
2. cos 2a= (cos^2 a) – (sin^2 a)
3. cos 2a= 1- 2 sin^2 a
4. cos 2a= 2 cos^2 a -1
5. tan 2a= ( 2 tan a) / ( 1- tan^2 a)
6. sin a/2= +/- sq. root of ((1 – cos a) / (2))
7. cos a/2= +/- sq. root of (( 1+ cos a) / (2))
8. tan a/2= +/- sq. root of (( 1- cos a) / ( 1+cos a))
9. tan a/2= +/- (( sin a) / ( 1+ cos a))
10. tan a/2= +/- (( 1- cos a) / (sin a))

Example: Simplify cos^2(4A) – sin^2(4A)
• Cos 2(4A)
• Cos 8A

-Braxton

10-1

So this week I am going to help you refresh your memory on problems using two different formulas. This is really easy! There are only two formulas that you need to you learn. These formulas are:

• cos (a +/- B) = cos a cos B -/+ sin a sin B
• sin (a +/- B) = sin a cos B +/- cos a sin B

Those are the two main formulas although they are some others you may need to know.

• sinx + siny=2sin(x+y/2) cos(x-y/2)
• sinx - siny=2cos(x+y/2) sin(x-y/2)
• cosx + cosy=2cos(x+y/2) cos(x-y/2)
• cosx - cosy=-2sin(x+y/2) sin(x-y/2)

Okay, so now that I gave you the formulas I am going to do a few examples for yall so yall can better understand how to work these problems.

Example 1: Find the exact value of sin 150 degrees

• Look at the trig chart to see if any of the degrees add or subtract to equal 150. Which is 90+60=150
• So you then plug it in the sin formula given above.
• You will then get Sin(90+60)=Sin90Cos60+Cos90Sin60
• After that you plug it all into the trig chart and get your exact value answer.
• And its that easy!

Example 2: Solve for sin75 cos15 + cos75 sin15

• All you do for this one is plug it into the formula that matches it from above.
• Which is sin(alpha + beta)= sin (alpha) cos (beta) + cos (alpha) sin (beta)
• You then should get sin(75+15)= sin 90 = 1 for your answer.

And that is it for this weeek. Have a happy new years!

-Halie

Review of Chapter 6

Other Notes for Chapter 6
-In this set of notes, we learned how to identify conics without using standard form.
-The equations are in the form of Ax^2 + Bxy + Cy + Dx + Ey + F = 0.
-To find the shape of the graph, you compute B^2 - 4AC.

• If it is a circle, you end up with a negative number, and A=C & B=0.


• If it is an ellipse, you get a negative number, and A does not = C & B does not = 0.


• If it is a parabola, you get 0.


• If it is a hyperbola, you get a positive number.

Example 1: Identify the graph of the equation x^2 - 2xy - y^2 = 4.

-A= 1 B= -2 C= -1

-(-2)^2 - 4(1)(-1) = 4 + 4 = 8

-8 is positive, so the graph is a hyperbola

Example 2: Identify the graph of the equation x^2 - 2xy + 3y^2 - 1 = 0.

-A= 1 B= -2 C= 3

-(-2)^2 - 4(1)(3) = 4 - 12 = -8

--8 is negative, A does not = C, and B does not = 0, so its an ellipse

easy review for christmas

ok so today will be really easy review because it is christmas so that will be your present. today we will be going over co-terminal and refernce angle. a positive coterminal angle is when you add or subtract 360 to get a positive number and a negative is when you add or subtract 360 to get a negative number. a refernce angle is when you add or subtract 360 or 180 to get an angle between 0-90 degrees to "refer" to the other angle.


EX:
positve and negative coterminal angle for 108 degrees
positve: 468 degrees   negative: -252



refernce angle for cos 135
=    - cos 45

MERRY CHRISTMAS

We're going to review some simple stuff today. The first thing we're going to review is reference angles.

Reference angles are really easy and they are needed at various times throughout your entire trigonometry life!

We learned this a few months ago, so you should remember how to do.

Incase you didn't, i'm going to review how to do it. It's very simple

Example 1:

Find the reference angle of Sin 120.

• Because Sin is y/r, you have to find out weather or not y's are negative or positive in the quadrant that 120 is in.
• Because sin 120 is in quadrant II, it is positive.
• Now you have to find the reference angle by making 120 negative and adding 180.
• You now get Sin 60.
• Simplify it completely and you get sqrt3/2

Example 2:

Find the reference angle of Cos 315

• Because Cos is x/r, you have to find out weather or not x's are negative or positive in the quadrant that 315 is in.
• Because Cos 315 is in quadrant 4, it is positive.
• Now you have to find the reference angle by making 315 negative and adding 360.
• You get Cos 45
• Simplify it completely and you get sqrt2/2

Merry Christmas to allllll and to all a good night! :)

Carley :)

Merry Christmas and Happy Ellipses.

So here’s the deal guys, I didn’t know what to blog about and the first thing I saw upon opening my binder was ellipses so that sounded like a good topic. Time to review.

Standard form of an ellipse is as follows:

x^2/a^2+y^2/b^2=1

Put an ellipse into standard form by dividing or completing the square. Dividing is a lot easier, trust me.

1.Define the major axis (The variable with the largest denominator is major)

2. Define the minor axis (The variable with the smaller denominator is minor)

3. Find the vertex. The vertex is the square root of the major axis (larger denominator).It is put into point form. The answer goes into the slot of the major axis.

4. Find the other intercept. The other intercept is the square root of the minor axis (smaller denominator). It is put into point form and the answer goes into the slot of the minor axis.

5. Find the length of the major axis. This is found by multiplying the square root of the major axis by two.

6. Find the length of the minor axis. This is found by multiplying the square root of the major axis by two.

7. Find the focus. (The focus is ALWAYS on the major axis.) It is in point form. The equation for finding the focus, vertex, or other intercept is smallest denom=largest denom-focus^2.

EXAMPLE

Sketch the ellipse.

X^2/49+y^2/64=1

1. Y is major.

Again, the larger denominator is the major axis.

2. X is minor.

The smaller denominator is the minor axis.

3. Vertex=square root of 64=+/-8 (0,8) (0,-8)

The vertex will always be the square root of the major axis put into point form and you better not forget that or I will be very upset with you.

4. Other intercept=square root of 49=+/-7 (7,0) (-7,0)

The other intercept is, obviously, always the square root of the minor axis put into point form.

5. 2*square root of 64=16

6. 2*square root of 49=14

7. 49=64-f^2
f^2=15
f=+/-square root of 15 (0, square root of 15) (0, square root of 15)

THE FOCUS IS ALWAYS ON THE MAJOR AXIS.

You would, of course, graph it afterwards.

That’s our review.

I hope everyone had a great Christmas and has an awesome new year. See you guys soon (:
--Sarah

8-1 Angle of Inclination

Finding the angle of inclination is quite simple when applying either formulas:

m=tan (theta) or tan2A=B/A-C

Some things to keep in mind when performing these types of problems:

- Make sure to isolate the trig function

- Always have a calculator by side because when you take the inverse of tan you will need it.

Here's an example:

Find the angle of inclination of 2x+5y=13

(If you remember that m= -A/B(i.e. 2 is A and 5 is B)

-2/5= tan theta so when isolated it's theta =tan (inverse) -2/5

(Hint: Do not stop and think after you have plugged this into your calculator that you are finished; you still have to find out what quadrants the answer can be found in)

So, when plugged into calculator you get theta = 21 degrees 48 minutes 4 seconds

Now, this isn't the answer because the slope is negative and the answer can only be found negative in quadrants II and IV

so make the quadrant I angle negative and add 180 degrees to it so it can be converted to a quadrant II angle.

When done, you should get 158. 199 degrees

To convert the quadrant I angle to a quadrant IV angle you must make it negative and add 360 degrees to it

When done, you should get 338.199 degrees

Convert these answers to degrees minutes and seconds and you are finished

So the answers are as follows 158 degrees 11 minutes 56 seconds

338 degrees 11 minutes 56 seconds

~Sameer

Reference Angles

First of all, you need to know that reference angles are like reduced fractions. They have to be between 0 degrees and 90 degrees.

Steps:

1. You have to find the quadrant and then sketch it.
2. Next, determine if it is a positive or negative angle by using the unite circle.
3. Then, subtract 360 degrees or 180 degrees from the original number until theta is between 0 degrees and 90 degrees.

Formulas you need to know:

• Sin(theta)=y/r
• Cos(theta)=x/r
• Tan(theta)=y/x
• Csc(theta)=r/y
• Sec(theta)=r/x
• Cot(theta)=x/y
  

Example 1: Find the reference angle for sin600

1. 600-360=240. 240 is in the third quadrant.
2. Sin=y/r=-1/1. So it is negative.
3. Now you have to subtract 240 from 180 which gives you 60.
4. Final answer: -sin60 degrees.

Example 2: Explain sin5Pi/4 as a reference angle.

1. First, you have to put the original problem in degrees. 5Pi/4 x 180/Pi=225 degrees.
2. 225 degrees is in the third quadrant. Sin=x/r=-1/1. So it is negative.
3. 225-180=45
4. Final answer: -sin45 degrees=-sinPi/4

Amber :)

7-4 Reference Angles!

Merry Christmas! :D I loveee Christmas!! So this weeeek I am going to do my blog on finding referencee angles! This is super easy, so it shouldn't take that longg.

Here are a few steps you need to know:

• First thing you have to do is find the original quadrant and sketch it.
• The next thing you need to do is figure out if the angle is positive or negative. You can use the unit circle the formulas: cos=x/r, sin=y/r, tan=y/x, sec=r/x, csc=r/y.
• The last thing you have to do is either subtract my 360 or 180 until the angle is in between 0 and 90.

So now that you know all that, I am going to work an example!

Example: Find the reference angle of sin 400 degrees.

• First you subtract, which gives you 220. That lets you know that it is in the thrid quadrant.
• It is going to be negative because sin is y and y in the third quadrant is negative.
• Then you subtract 220 from 180 and get 40.
• Your final answer is going to be -sin 40 degrees.

And thats it for this weeeek! Have a happy holidays!

--Halie! :D

10-1 and 10-2 Review

This weekend I am going to review with you all the material that we learned in chapter 10 sections 1 and 2. Basically, all you need to know for this section is formulas. You also need to know your trig chart. You will be referencing back to the trig chart to plug into the trig formulas. Sections 1 and 2 are about addition and subtraction. Now to give you the formulas required for this section.

Formulas:
1.cos (alpha +/- beta) = cos (alpha) cos (beta) -/+ sin (alpha) sin (beta)
2. sin (alpha +/- beta) = sin (alpha) cos (beta) +/- cos (alpha) sin (beta)
3. sin x + sin y = 2 sin ((x + y)/(2) cos ((x-y)/(2)
4. sin x - sin y = 2 cos ((x+y)/(2) sin ((x-y)/(2)
5. cos x + cos y = 2 cos ((x+y)/(2) cos ((x-y)/(2)
6. cos x - cos y = -2 sin ((x+y)/(2) sin ((x-y)/(2)
7. tan (alpha + beta)= ((tan alpha + tan beta)/(1- tan alpha tan beta))
8. tan (alpha – beta)= ((tan alpha – tan beta)/(1+ tan alpha tan beta))

Example: Simplify cos 2x cos x + sin 2x sin x
• Cos (2x-x)
• Cos x

-Braxton

REVIEW OF 10-1

Formulas for cos(a +/ B) & sin(a +/ B)

Today, I will be reteaching you lesson 10-1 where we learn the sum and difference formulas for Cosine and Sine. The formulas are as follows:

-cos(a +/- B) = cosa cosB -/+ sina sinB

-sin(a +/- B) = sina cosB +/- cosa sinB

*When using these formulas, we get our values straight off the trig chart.

Example 1: Find the exact value of sin 15 degrees.

-sin(45 - 30) = sin45cos30 - cos45sin30

-(sq root of 2/2)(sq root of 3/2) - (sq root of 2/2)(1/2)

-(sq root of 6/4) - (sq root of 2/4)

=((sq root of 6) - (sq root of 2)/4)

Example 2: Find the exact value of cos 75 degrees.

-cos(45 +30) = cos45cos30 - sin45sin30

*Now you replace the sin and cosine values with the trig chart values.

-(sq root of 2/2)(sq root of 3/2) - (sq root of 2/2)(1/2)

=((sq root of 6) - (sq root of 2)/4)

Example 3: Find the exact value of cos50cos10 - sin50sin10.

-cos(50 + 10)

-cos(60)

*Replace cos60 with its trig chart value.

=1/2

11-2

today is changing polar complex numbers to rectangular complex numbers. the formula is in 11-1 and your answer should come out as z= x + yi. it is not that hard to do but is easy to mess up. all you do is change it from polar to rectangular the what ever is x goes first and whatever is y goes next to the i. here is an example below.

EX:

6 cis 100

x= r cos (theta)   y= r sin (theta)

x= 6 cos 100    y= 6 sin 100

x= -1.042        y= 5.91

z= -1.042 + 5.91 i

I JUST LOVE DOING BLOGS ON MY SUNDAYS

7-1

I'm going to be reteaching lesson 1 of chapter 7 where we learn how to convert between degrees and radians, and how to find co-terminal angles.

• When working with degrees, you often get a decimal answer. When you get a decimal, you are usually told to convert to minutes(') and seconds("). To convert to minutes, you take what's following the decimal, and multiply it by 60. To convert to seconds, you take what is following the decimal in your answer for minutes, and multiply it by 60.
• To convert minutes and seconds to degrees, you do the following: (degree + min/60 + sec/3600)
• To convert from degrees to radians, you do the following: (degree x pi/180)
• To convert from radians to degrees, you do the following: (radians x 180/pi) *pi cancels out
• To find a co-terminal angle in degrees, you do the following: (+/- 360)
• To find a co-terminal angle in radians, you do the following: (+/- 2pi(n))

Example 1: Convert 16.33 degrees to degrees/min/sec.

-.33 x 60 = 19.8'

-.8 x 60 = 48"

= 16 degrees, 19', 48"

Example 2: Convert 60 degrees to radians.

-60 degrees x pi/180 = pi/3

Example 3: Convert 3pi/4 to degrees.

-3pi/4 x 180/pi = 135 degrees

Example 4: Find a co-terminal angle to pi/4.

-pi/4 + 2pi = 9/4pi

cheers to the freakin weekend

I am going to be reviewing 7-2. These steps and formulas are most commonly used to solve different word problems. There are several formulas that you will have to remember in order to properly solve these word problems.

The first formula is as follows:
K=1/2r^2 Ɵ

In this equation, k is the area of a sector, r is the radius, and Ɵ is the central angle.

The second formula is follows:
K=1/2rs

In this equation, r is the radius, and arc is the length.

Another equation within this section is that for apparent size. That equation is as follows:
s=rƟ

In this formula, r=distance between two objects, Ɵ=apparent size, and S=diameter of an object.
EXAMPLE 1:
A sector of a circle has a radius 8 cm and central angle 2 radians. Find its arc length and area.

In this problem,
R(radius)=8cm
Ɵ(central angle)=2
K(area)=?
S(arc length)=?

To solve this problem, you would use the equation k=1/2r^2Ɵ.
Therefore, k=1/2(8)^2(2) so k=64cm^2.

You then plug into k=1/2rs. Since you’re solving for s, it becomes k/1/2r=s.

Therefore s=64/4 so s=16cm.

So, in the end the arc length (s) is 16cm and the area (k) is 64cm^2.
--Sarah

TRIG REVIEW

Today we are going to do some review from the trigonometry section. If you do remember Trig, you are good to go and can probably work my examples right now. But incase you don’t remember everything; all you need to know right now in trig is basically formulas as well as the trig chart. For starters, you must remember:

· Sin=1/csc

· Cos=1/sec

· Csc=1/sin

· Sec=1/cos

· Tan=1/cot

· Cot=1/tan

· Tan=sin/cos

Apart from knowing that, you must also know the Pythagorean Identities. To refresh your memories, these are the Identities you will need to use when doing a lot of trigonometry.

· Sin^2+cos^2=1

· 1+tan^2=sec^2

· 1+cot^2=csc^2

Now that we’ve went over some of the basic things needed to work the examples I am about to show you, we can begin J

Example 1: Simplify:

(Sinx^2+Cosx^2)/ Sinx

1. Look for identities. You have one, so simplify it.

2. You now get 1/Sinx. You can simplify this by referring to the notes above.

3. You get Cscx as your final answer J

I hope this review helped!

CARLEYYYYY

7-4

So this week I'm going over a section we learned in chapter 7. Reference angles are just like reduced fractions. The purpose of them are to make an angle you have bigger than what you need and and shrink it. The steps for making a reference angle are as follows:

1. Find the original quadrant

2. Determine if the angle is a positive or negative angle ( you have to refer back to the unit circle for this)

3. Subtract 360 degrees or 90 degrees until you get the angle between 0 degrees and 90 degrees

Example timeeee!!!!

Example 1: Find the refernce angle of sin 695 degrees

First you have to find out which quadrant 695 degrees lies in.

sin 695 degrees lies in quadrant 4

Now using the unit circle we have to determine if sin 695 degrees is positive or negative

Since sin = y/r the y in the angle is negative

Sin 695 degrees is negative

Now you will subtract 360 degrees until you get the angle between 0 and 90 degrees

sin 695 degrees = -sin 25 degrees

Example 2: Find the refernce angle of cos 725

cos 725 degrees lies in quadrant 1

cos 725 degrees is positive

cos 725 degrees = cos 5 degrees

Welp, that's it!!(:

7-1 Converting

When you are converting from degrees to minutes and seconds:

• When converting to minutes, take the numbers or number behind the decimal and multiply it by 60.
• When converting to seconds, you take the answer you got for minutes and multiply the numbers or number behind the decimal by 60.

Ex. Convert 14.65 degrees to minutes and seconds.

• .65 x 60=39
• Since the answer is not in decimal form, you do not need to go on to seconds.
• Final answer: 14 degrees 39 minutes

When you converting from minutes and seconds to degree:

• Take the degree and add it to minutes.
• Then you divide that by 60.
• Take that and add it to seconds and then divide by 60.

Ex. Convert 21 degrees 10 minutes 3 seconds to degrees.

• 21 + 10/60 + 3/60 = 0.059 degrees

When you are converting from degrees to radians:

• Take the degrees and multiply it by Pi/180.

Ex. Convert 200 degrees to radians.

• 200 degrees x Pi/180 =10/9Pi

When you are converting from radians to degrees:

• Take the number and multiply it by 180/Pi.

Ex. Convert 5Pi/9 to degrees.

• 5Pi/9 x 180/Pi
• The Pis cancel and leave you with 5/9 x 180
• Final answer:100 degrees

Amber :)

8-1 angle of inclinationnn

I am going to do my blog on angle of inclination..wooohoooo! There are ALOTT of notes for these types of problems. So i guess i should start giving you some of the notes. So here it goes:

• The first thing you want to do is isolate the trig functions. Which you should already know how to doo.
• The next thing you need to do is take the inverse of the trig function.
  
• The next step can be one of two things. You either can plug into the trig chart or just plug the equation into your calculator. EASYYY
• Then your going to use the quadrants to find the rest of your answes.

Some formulas for this section are m=tan a and tan 2a=B/A-C.

So i guess i should do some examples now. Or maybe ill just do one example.

Find the angle of inclination of 4x+8y=16

• use the formula m=tan a
• your slope is going to be -4/8
• so you can then plug that into the equation.
• which is going to give you 26.565.
• then you are going to plug it into the right quadrants and turn your answers into degrees minutes and seconds.
• your answers are going to be 153 degrees 26 minutes 6 seconds and 333 degrees 26 minutes 6 seconds.
  

and thats itt. LOVEE, BRADDD

8-4 Review

This week I am going to review with you all the material that we learned back in September. I am going to show you all how to work problems by using the relationships among trig functions. There are some formulas that you need to know before you work any problems.
Formulas:
• Sinx / cosx = tanx
• Cosx / sinx = cotx
• Cscx = 1 / sinx
• Secx = 1 / cosx
• Cotx = 1 / tanx
• Sin^2x + cos^2x = 1
• 1 + tan^2x = sec^2x
• 1 + cot^2x = csc^2x
• Sinx = cos (90 degrees – x)
• Cosx = sin (90 degrees – x)
• Tanx = cot (90 degrees – x)
• Cotx = tan (90 degrees – x)
• Secx = csc (90 degrees – x)
• Cscx = sec (90 degrees – x)
There are also some steps that you need to follow loosely.
Steps:
1. Algebra
2. Identites; try the Pythagorean identity first, then, if it helps, move everything to sin and cos
3. Then more Algebra
4. Continue with steps 1-3
Example: (secx – 1) (secx + 1)
• Sec^2x – 1
• Tan^2x

-Braxton

Converting Radians and Degrees

So this week we didn't learn anything new. So I am going to review how to convert radians to degrees and degrees to radians. I can't remember if I did these types of problems or not. So, I am just going to explain it again. It is really easy so it isn't going to take that long to explain it! So here it is.

There are a few easy steps you need to know when working these problems.

• To convert from radians to degrees you would use the formula, radians x 180/Pi
• To convert from degrees to radians you would use the formula, degrees x Pi/180

Note: All formulas require radians and radians are the preferred way to measure angles.

Now I am going to work a few examples for you.

Example 1: convert 315 degrees to radians

• 315 x Pi/180=7 Pi/4

Example 2: convert -3 Pi/2 to degrees

• -3 Pi/2 x 180/Pi=270 degrees

And it is as easy as that! So that is it for this week. BYEEE

--Halie

Subtracting Matrices

This is also quite simple but don't let the negative sign and minus sign confuse you when working this (Remember COPY-CHANGE-CHANGE) Also check to see if both matrices have the same dimensions. If they don't, the answer is not defined. If they have the same dimensions, then here is how you work the problem.

Example: [7 3 -4] - [6 4 3]

First, check to see if the dimensions are the same for both.

Second, determine what dimesions should be placed for your answer.

Finally, subtract the corresponding column or row with the corresponding row or column.

7 -6=1

3-4=-1

-4-3=-7

The answer is [1 -1 -7]

14-1

14-1 Matrices
So, I definitely almost forgot about my blog. In this section, we learn how to add and subtract matrices. We also learn how to do scalar multipication. You will also be given directions to transpose matrices. Here are some rules for this section:

• When adding or subtracting matrices, the matrices must have the same dimensions. NO EXCEPTIONS!


• To add/subtract matrices, all you do is add/subtract correspoding entries.


• To use scalar mutipication, all you do is multiply every entry by the number outside the matrices.


• When you are given directions to transpose a matrices, you will see A^t. All you have to do is switch the rows and the columns

Example 1: [3 4 -1] + [6 -3 2] = [9 1 1]

-Add 3 and 6, 4 and -3, -1 and 2, then you get [9 1 1]

Example 2: 4[2 1 6 -3] = [8 4 24 -12]

-Multiply 4 by 2, 1, 6, and then -3, and you get [8 4 24 -12]

Example 3: A = [4 2 6 1] B = [8 4 -2 5]; Find 2A - B.

-2[4 2 6 1] - [8 4 -2 4] = [-8 -4 -12 -2] - [8 4 -2 4]

= [-16 -8 -10 -6]

i almost forgot to do this.

This week I am going to talk about multiplying matrices. Pay close attention to this concept because it WILL be on the exam.

In order to multiply matrices, the dimensions have to be precise. You must have the same number of columns in the first matrix as rows in the second matrix. If you do not have such dimensions, YOU CANNOT MULTIPLY. If you do not have proper dimensions, the answer is not defined. DO NOT CONFUSE THIS WITH UNDEFINED. Undefined means you have divided by zero. NOT DEFINED means no solution.

-Helpful hint, after multiplying, your answer matrix will have the same number of rows as the first matrix and columns of the second matrix(:

HERE WE GO WITH THE EXAMPLE.

[3 4] [2 3 1] [22 33 23]

[6 7] X [4 6 5] = [40 60 41]

[9 1] [22 33 14]

Since the dimensions of the first matrix are 3x2 and the dimensions of the second matrix are 2x3, your answer matrix will be a 3x3.

First, multiply row one by column one. (I’m going to fill answers into the matrix as I go)

3(2)+4(4)=22

First row second column, then first row third column.

3(3)+4(6)=33 3(1)+4(5)=23

Continue the same process with rows two and three.

That’s all there is to it. Good luck to everyone taking the exam on Thursday. You can do it(:

--Sarah

This week I am going to teach some more about Matrices.

Since we did addition last week, we are going to move up to multiplication.

The first thing you need to know about multiplying matrices is when looking at dimensions of the two you are trying to multiply B and C MUST be the same number.

You use the term AxB CxD to check for this.

When multiplying, you multiply each number in the first matrix’s row by each number in the second matrix’s column.

After doing this you will add the numbers from which you multiplied each row by column.

The rows and columns that you multiply is going to be where you place the number in the answer matrix.

Now for an example of how to multiply matrices:

Example 1:

[1 2 3 -2] X

2

0

-1

3

1(2)=2

2(0)=0

3(-1)=-3

-2(3)=-6

So you answer matrix is going to be,

2 0

-3 -6

Hope you learned how to multiply matrices!

---Carley :)

yay for blogs

This week i am doing my blog on MATRIX MULTIPLICATION!!! YAY!!!

Notes:
-To Multiply Matrices, you have to look at the dimensions of each matrix to see if it is even possible first.
a x b b x c
-The two inner numbers of the dimensions must match for you to be able to multiply.
-The resulting matrix will be the two outside numbers.
a x c

Example: Multiply matrix {2 4} by matrix {4}
{3 1} {2}

2 x 2 2x 1

the inside numbers match and the answer will be a 2 x 1 matrix

Now you do 2 x4 + 4 x2 = 16
Next is 3x 4 + 1 x 2= 14

The end matrix is {16}
{14}



YaY we did it!! goodnight everyone

Matrix Multiplication

This week I am going to teach you all how to multiply matrices. The bigger the two matrices are, the longer it takes to multiply them. There are a few things you need to know before you multiply matrices.

Notes:
• To be able to multiply matrices, the inner numbers of the two dimensions have to match. For example 2x3 3x2; you would be able to multiply these two matrices. Ex. 4x3 2x4; you would not be able to multiply these two matrices because the middle numbers are not the same (if this happens your answer will be not defined).
• The dimensions of the answer will be the outer two numbers. For example, 4x3 3x4; the dimensions of the answer would be 4x4.
• You multiply each row by each column
Now I will work an example of a matrix multiplication problem.

Example: [4 5] x [6
.............................3]
• First you would check the dimensions: 1x2 2x1; the resulting matrix will be a 1x1
• Next you would multiply 4 (6) + 5 (3)
• Your answer would be [39]

-Braxton

Multiplying Matrices

Things you should know:

• Inner numbers must match. So what that means is if you have a 4x4 and a 2x4, you can't multiply those together. You can't multiply them together because the 4 and 2 are not the same. Only multiply it when they are the same.
• Your answer will be the outer numbers. So if you were give a problem with the matrices 3x3 and 3x2 then your resulting matrix would be 3x2.
• If you can not multiply a matrix, it is called "not defined".

Example 1:

• First, you have to see what dimensions they are. Both of them are 2x2.
• Second, you have to see if the inner numbers match, which they do.
• So, you multiply 6x3+-5x2=8, 6x-1+-5x4=-26, 0x3+1x2=2, 0x-1+1x4=4.
• Final answer:

Example 2:

• First, find the dimensions of each matrix. 2x2 and 3x2.
• The inner numbers are not the same.
• You are not able to multiply these matrices.
• Final answer: Not Defined.

:) Amber

Matrix Multiplication!

This week my blog is going to be on multiplying matrices.

• In order to multiply matrices the inner numbers have to match. For example if you have a matrix with 3x4 dimensions and another matrix with 4x2 dimesnions, that can be multiplied because the two inner numbers are 4 and 4.If you have a matrix with the dimesnions of 2x3 and another with 2x3 they will not be able to multiply because the inner numbers are 3 and 2.








• When you multiply the matrices, the resulting matrix will have dimesnions of the outer numbers.

Now I'm going to do some expamples to help you better understand.

Example 1:

The dimensions of matrix one is 2x3. The dimensions of matrix two is 3x2. Because the inner numbers match, they can be multiplied. Now you multiply

This is is your final product.

Example 2:

Because the inner numbers of the dimesnions of the matrices don't match. This cannot be multiplied. So your answer is not defined.

Ta-da!! There you have it!

Matrix Multiplication

So, this week I am going to do my blog on how to mulitply matrices. It takes a long time but it is very simple. First, I am going to give you a few notes that you will need to know to be able to mulitply matrices.

Note:

• When you mulitply matrices the inner numbers have to match. For example, if you are multipling a 2x3 and a 3x4 then you are able to mulitply it because the inner numbers match.
• Your resulting matrix will be the outer numbers. So working with the problem above, your resulting matrix will be 2x4.
• If your inner numbers do not match then you will not be able to mulitiply them and your answer will be not defined.

So now I am going to work a few examples for you to better understand these types of problems.

Example 1:

• The dimensions of these two are 2x2 and 2x1. The inner numbers match so you are able to mulitiply it.
• You are going to mulitply 4(5)+3(5)=35 and -1(5)+-2(1)=-7
• Your answer is going to look like this:
• 

Example 2: Mulitiply two matrices with the dimensions 2x1 and 2x2.

• You cannot mulitiply these two matrices together because the inner numbers are 2 and 1 and they do not match.
• So your answer is going to be not defined.

And that is it for this weeek! GOOOODBYEEE :D

--Halie

Ok soo today im going to explain how to do a few things with matrices. im going toi show you how to transpose. which is represented by m raised to t. which is also represnted by m^t. I will also show you how to multiply matrices. The most important thing about multiplying matrices is you have to make sure the 2 inner number are the same 2x3 3x2 and this will result in a 2x2 matrix. Next i will show you an example or two of each one.

This is an example of how to transpose a matrix:
[2 3] = [[2]
[3]]

[[3]
[2]]= [3 2]

This is and example of how to multiply a matrix:

[[7]
[2]] x [2 3] = [[14 21]
[4 6]]

11-1

this is a review from the first section of chapter one. this is converting rectangular to polar and polar to rectangular. to convert rectangular to polar the do [r =(the square root of) x^2 + y^2] then you do [ (tan inverse) y/x]. to go from polar to rectangular you do [x= (r cos (theta) ) and y= r sin (theta) ]. its really easy so lets get an example going.




EX: give polar coordinates (-2,2)
 first r= (the square root of) 2^2 +2^2
you get (square root of) 8 = 2 (square root of) 2
second is (tan inverse) 2/-2 = (tan inverse) -1= 45 (degrees)
tan is -ve in 2nd and 4th quadrant so its is 135 and 315
-2,2 is in Q2 which is where 135 is
answer is [2(square root of) 2, 135 (degrees)] and [-2 (square root of) 2, 315 (degrees)]


give rectangular coordinates (4,120(degrees) )
first x=4 cos 120 and y=4 sin 120
4(-.5)= -2        4(square root of) 3 / 2 = 2 (square root of) 3
answer is (2, 2(square root of) 3)

Matrices!

So I know I'm posting this kind of late but I forgot all about it, but hey, it's still Sunday. So I'm going to talk through how to add matrices and what not. This is a really simple section, so it shouldn't be that hard. To add matrices they must be the same dimensions, which simply means that the row x column must be the same. To complete secular multiplication you multiply every entry by the number. A^t means tranpose. This simply means that you switch rows and columns.
As we all know it's time for the examples

Example 1: [3 4]
1 0
5 -2

Find m^t

All you have to do is switch the rws and colums

[3 1 5]

4 0 2

This is the blog from the thanksgiving holidays i forgot to do

Hi its the the "Cory Doesnt Feel Like Doing Blogs Show" again.
On this blog im gonna multiply matrices.

Dimensions: a x b b x c inside numbers must be same to multiply

A= (4 5) B= (6)
(2 1) (3)

4 x 6 +5 x 3= 39
2 x 6 + 1 x 3= 15

(39)
(15)

YAY!! I DID IT !!!
Hercules hercules!!

EW BLOGS

Hi and welcome to the "Cory Doesnt Feel Like Doing Blogs Show" !! (crowd goes wild)

im not doing an intro because i dont feel like it!!
Okay? Come at me bro

Were gonna add matrices. To add matrices, add corresponding parts

Example: A= (6 5 4) B= (4 5 6)
(3 2 1) (7 8 9)

Add corresponding parts:
6 + 4= 10
5 + 5= 10
4 + 6= 10
3 + 7= 10
2 + 8 = 10
1 + 9= 10

A + B= (10 10 10)
(10 10 10)

Yay!! I did it!

14-1 Matrices

I am going to teach about how to add matrices. It's quite simple but here a few things to keep in mind while performing this simple algebra.
• Must have the same dimensions, if you are adding or subtracting.
• The corresponding numbers are added or subtracted in the matrices.
• Another thing that you need to remember is that you add or subtract the corresponding numbers in the matrices
• A^t means to find the transpose of A. Just switch the rows and columns of the matrice.

Example: [ 9 12 ] [ 6 3 ]

+

[ 15 8 ] [ 7 5 ]

To find out the answer:

Add the corresponding first row first # to the corresponding first column first #

So, 9+6=15

Add the corresponding first row second # to the corresponding first column second #

So 12+7= 19

Add the corresponding second row first # to the corresponding second column first #

So 15+6= 21

Add the corresponding second row second # to the corresponding second column second #

So 8+5=13

The dimensions of the matrix is 2x2

The final matrix would be [ 15 19 ]

[ 21 13 ]

14-1

Chapter 14 is all about matrices. A matrix is a group or set of numbers. Today wet are going to learn the basics of matrices. We're going to learn how to tell the dimensions, how to add and subtract, and how to transpose(^t).

The first thing we're going to learn is how to tell dimensions. You do this by counting the number of rows and columns. You then put it in the form (rows x columns)

Example: 2 -5 10

-4 19 4

The dimensions would be 2x3

Te next thing we're going to learn is how to add/ subtract matrices. All you do is add or subtract the corresponding numbers. THE MATRICES MUST HAVE THE SAME DIMINSIONS!

Example: (2 6 -2) + (-2 5 0)

Answer: (0 11 -2)

The last thing we're going to learn is how to transpose. All you do for this is switch the rows for columns and columns for rows.

Example: what is (2 3 -2)^t?

Answer: 2

3

-2

And that all there was in section 1! Hope you leanred something!

Carleyyyy :)

This week, on the few days we were not testing, we learned about matrices. It is a rather simple concept. I am going to talk about the addition of matrices.

-A^t means transpose. That simply means switch the rows and columns.

-To add matrices they must be the same dimensions (number of rows and columns)

-To complete scalar multiplication you multiply every entry by the number.

EXAMPE TIIIIIIIIIIIIME

M= [7 1 5]

[4 3 2]

A. What are the dimensions of the matrix?

2x3 ( There are two rows and three columns )

B. Find m^t

[4 7]

[3 1]

[2 5]

Example TWO:

Add the matrix from the last example and the matrix

[8 3 4]

[6 2 9]

Simply add the corresponding spots.

[7+8 1+3 5+4]

[4+6 3+2 2+9]

The answer would then be:

[15 4 9]

[10 5 11]

So that is how you work with matrices.

--Sarah (:

matrices

Soooo here i sit on a sunday night. There is soooo many things that are better than this that i can be doing. Like watching tv or thinking about how much i hate school. any way i guess i will get started on this blog.

A^t which means transpose= switch rows and columns.

to add matricies they must be the same dimensions(row and columns)

to add matricies you add corresponding enties.

to complete scalar multiplication you multiply every entry by the number.

These are a few simple steps you can follow to help you. Now i will show a few examples.

[1 -1 0]+[6 -9 -1]=[7 -10 -1]

4[2 4 6 3] = [8 16 24 12]

Adding Matrices

In order to add -or subtract- matrices, one must have equivalent dimensions; so if your adding these: [2 14 53] + [2 33 21 15] you are not able to because the dimensions are not the same.

Ex. [1 14 52] + [11 32 85] (add the corresponding numbers -row one column one with row one column one etc.) = [12 46 137]


~ Parrish Masters

Matrices

This week I am going to teach you all how to work problems with matrices. This is one of the easiest things that I will teach you this year. It is pretty much basic algebra.

Here is a list of things that you need to know about matrices:
• Whenever you add or subtract matrices, they must have the same dimensions
• The dimensions are (rows x columns)
• Another thing that you need to remember is that you add or subtract the corresponding numbers in the matrices
• When you see, find A^t, it means find the transpose of A. Transpose means to switch the columns and the rows of the matrix.

Now it is time for me to show you an example.

Example: [ 5 13 ] + [ 15 8 ]
• You would add 5 + 15 and 13 + 8
• Your final matrix would be [ 20 21 ]
• The dimensions of this matrix are 1 x 2


-Braxton

Matrices

This week we learned about matrices. They are very simple.
You should know that before we start, we have some rules to go over.

Rules:

• When adding matrices, they have to be the same dimensions. (The rows and columns have to be the same. Rows x Columns).
• When you add the matrices, you add the corresponding entries together.
• Whenever you see A^t in a question/problem, it means to switch the rows and columns.

Example 1: [5 10] +[25 8]

• First, you have to see which ones are corresponding entries.
• 5 and 25 are corresponding and 10 and 8 are corresponding entries.
• Now you add those together. 5+25=30 and 10+8=18.
• Final answer: [30 18]

Example 2: What is the dimensions of [6 15 9]?

• First thing you should know is that dimensions are rows x columns.
• As you can tell this problem has one row and three columns.
• Final answer: 1x3

Example 3: Find A^t of

• So like I said above in the rules, A^t means to switch the rows and columns.
• This means you are finding a transpose of the original problem given.
• So the final answer is:

Example 4: Find 6M for [3 7 9].

• First, all you need to know is you will be multiplying 6 to each number.
• 6x3=18, 6x7=42, and 6x9=54
• Final answer: [18 42 54]

-Amber :)

Matrices!

This week I am going to teach you how to work matrix problems. They are really easy! There are a few things you need to know though before I begin working examples.

These few things are:

1. To add matrices they must be the same dimensions (rows x columns)
2. Also, when you add matrices, you always add the corresponding entries.
3. A^t is a type of matix. ^t means to swith rows and columns.

So now that you know the basics. I am going to work some examples for you.

Example 1: [ 12 7] + [3 -4]

• When adding matrices, remember that you add the corresponding entries.
• So it is going to be 12 + 3 and 7 +-4.
• Your answer is going to be [15 3]

Example 2: What are the dimensions of the answer of the problem in example 1?

• To figure out the dimensions it is very easy.
• Dimensions are always written rows x columns.
• So the answer to example one was [15 3]
• You have one row and two columns in that answer
• So your dimensions are going to be 1 x 2

Example 3: [15 3]^t

• In this problem you are going to be finding the transpose of the given problem.
• This is very easy! All you have to do is swith the rows and columns.
• So your answer is going to be | 15 |
• | 3 |

And that is how you work problems with matrices! YAYYY.

--Halie!

14-1

14-1 Matrices
In this section we learn how to add and subtract matrices, and multiply matrices using scalar multipication. This is all very simple, and there's only a few things to remember in this section:

• The matrices being added/subtracted must have the same dimensions (row x column).



• To add matrices, you add corresponding entries. Do the same when subtracting.



• To use scalar multipication, you multiply every entry by the outside number.




• A^t means transpose, which is where you swich the rows and columns.

Example 1: [2 -6] + [3 4] = [5 -2]

Example 2: [9 5] - [-1 2] = [10 3]

Example 3: Find 4A. A = [3 2 -5]

4[3 2 -5] = [12 8 -20]

Example 4: Find 2A + B. A = [4 7] B = [-2 6]

2[4 7] + [-2 6] = [8 14] + [-2 6] = [6 20]

--Jordan:)

matrices

today is one of the easier blogs where i teach you how to add matrices. sounds easy right? well it is. the only catch is that the matrices have to have the same dimensions such as 2x3 and 2x3. you can add those however you cannot add 2x3 and 3x2 because they do not have the same dimensions. lets look at our example below to see how simple this is.


[12   7] + [3   -4]

add 12 and 3 and get 15.
add 7 and -4 and get 3.
answer is [ 15   3]

11-1

This is how to convert from Polar to Rectangular.

There are two formulas to use when converting.

Here are the two formulas to use

• x= r cos(ø)
• y= r sin(ø)

Instead of (x,y) it is (r,ø).

Example 1:

Convert (3,45º) to rectangular.

1. x=3cos45º, so x=1.576
2. y=3sin45º, so y=2.553
3. The rectangular coordinates are (1.576, 2.553)

-Sameer

6-4

This week is a golden opportunity to review hyperbolas. I am sure some of you remember this, but others of you may not so here we go with the blogging and the teaching and what not.

Standard form!

x^2/a^2-y^2/b^2=1 OR -x^2/a^2+y^2/b^2=1

1. Major axis is bigger denominator (i.e. positive)

2. Minor axis is smaller denominator (i.e. negative)

3. The vertex is square root of largest denominator (in point form the answer goes in place of the major axis)

4. The other intercept is the square root of the smallest denominator (see above for point form)

Steps 5 and 6 are unnecessary for hyperbolas.

7. f^2=larger denominator+smaller denominator OR f^2=vertex^2+other value^2

8. Asymptotes

y=+/- square root of y denom/square root x denom x

At the end you graph it, but I won't be doing that.

EXAMPLE

-x^2/16+y^2/36=1

1. y is major

2. x is minor

3. square root of 36=6

4. square root of 16=4

5 and 6 are still unnecessary.

7. f^2=16+36

f=square root of 52 or +/-2 square root of 13 (0,2square root 13)(0,-2square root 13)

8. y=+/-6/4= +/-3/2

Don't forget to graph after.

--Sarah

11-3

11-3 Powers of Complex Numbers
This week I will be reviewing how to find powers of complex numbers. We use De Moivre's Theorem to find these roots. It's simpler to find powers of a complex number when the complex number is in polar form.
De Moivre's Theorem:
If z = r cis theta, then z^n = r^n cis n(theta).

*In this section, you will not draw Argand diagrams.*

Example 1: Evaluate (2 cis 45 degrees)^2.

• z^2 = 2^2 cis 2(45 degrees)


• z^2 = 4 cis 90 degrees

Example 2: z = 3 cis 10 degrees. Use De Moivre's Theorem to find z^3.

• z^3 = 3^3 cis 3(10 degrees)


• z^3 = 27 cis 30 degrees

Example 3: If z = 1 + c, find z^4.

• z = x + yi


• r = sq. root of x^2 + y^2


• r = +/- sq. root of 2


• theta = tan^-1(y/x)


• theta = 45 degrees, 225 degrees


• z = sq. root of 2 cis 45 degrees


• z = sq. root of 2 cos 45 degrees + sq. root of 2 sin 45 degrees(i)


• z = - sq. root of 2 cos 225 degrees


• z^4 = sq. root of 2^4 cos 4(45 degrees)


• = 4 cis 180 degrees


• = r cos 180 degrees + 4 sin 180i

11-2

11-2 has problems that use complex numbers.
Formulas you need to know:

• z=x+yi
• z=rcos(theta)+rsin(theta)i
• z=rcis(theta)
• z=square root of x^2+y^2

When multiplying complex numbers:

• If it is a rectangular problem, you always use foil.
• If it is a polar problem, you always multiply r and add theta.

Example 1: 5+2i

• First, you have know if it is in rectangular form or polar. It is in rectangular form.
• Now, since you know it is in rectangular form, you know you will have to find r and theta.
• Use the formulas from above ^^^^^. To find r, you have to use the r=square root of x^2+y^2 formula.
  
• Put the numbers in the formula and solve: R=square root of 5^2+2^2=square root of 25+4=square root of 29. (i always equals 1)
  
• Now, you have to find theta by using the formula Theta=tan^-1(y/x).
• Put the numbers in the formula and solve: Theta=tan^-1(2/5)=21.801 and then you have to put it in quadrant one and then find the other answer which is 201.801.
• You can now put your answers in their final form: square root of 29cis21.801 and -square root of 29cis201.801.

Example 2: 8cis240 degrees

• Like the problem above, you have to know which form this equation is in. It is in polar form.
• Since it is in polar form, you now know that you have to find x and y.
• You have to use the formulas x=rcos(theta) and y=rsin(theta).
• Since the degrees in the original problem is not between 0-90, we have to find a reference angle. 240-180=60.
• Now you can place the numbers in the formulas.
• X=8cos60=8(1/2)=4
• Y=8sin60=8(square root of 3/2)=6.928
• Your final answer is z=4+6.928

-Amber :)

11-2

Today I'm going to teach 11-2, which involves solving problems using complex numbers. This is a fairly easy section. There are a few formulas. They are:

z = x+yi (in rectangular)

z = rcos(theta)+rsini OR rcis(theta) (in polar)

z = square root of x^2+y^2

Remember that i = square root of -1 and cannot be simplified.

To multiply complex numbers you must: 1. foil (if expressing in rectangular) 2. multiply r and add theta (if expressing in polar)

Now I have examples to help work out these problems.

Example 1: Express in polar form.

3-4i

First we need to find r and theta. This is when the formulas from 11-1 come back.

r = square root of 3^2 + (-4)^2

r = +/- 5

theta = tan^-1((-4)/3)

theta = 307 degrees7'48" , 127 degrees7'48"

Now we have to write it out in polar form. To do this you have to find out which quadrant your original formula falls in. Then that's how you determine which r go with which theta. Since 3,-4 falls in the foruth quadrant so r=5 and theta=307 degrees7'48" goes together. Your answers are:

z=5cis307degrees7'48"

z=-5cis127degrees7'48"

Example 2: Express in rectangular form

6cis100 degrees

In order to do this you have to find x and y first. Once again, formulas from 11-1 are going to be used again.

x = 6cos100 degrees

x = -1.04

y = 6sin100 degrees

y = 5.909

Now you just write the answer like an formula.

z = -1.04 + 5.909

-danaaaa(:

11-2

This week I am going to teach you all chapter 11 section 2. The problems in this section use complex numbers. There are several formulas that you need to know so that you can work problems in this section.
The formulas are as follows:
• z = x + yi
• z = r cos theta + r sin theta i
• z = r cis theta
• z = square root of ( x^2 + y^2 )
Remember, when multiplying complex numbers:
• To multiply rectangular equations, use FOIL
• To multiply polar equations, multiply r and add theta
Now I will show you an example of how to do one of these problems.
Example: Change ( 3, 3 ) from rectangular to polar
• r = sq. root of ( 3^2 + 3^2 )
• r = +/- 3 sq. root (2)
• theta = tan^-1 (3/3)
• theta = 45 degrees, 225 degrees
Your final answer would be (3 sq. root of 2, 45 degrees) and (-3 sq. root of 2, 225 degrees)

-Braxton-

11-1

So this week I am going to do my blog on 11-1, which has to do with polar problems. These problems are really easyyyyy. Polar problems are always (r, theta) and rectangular problems are always (x,y). There are a few formulas for these types of problems. So I am going to give you these formulas right nowww.



x=rcos theta
y=rsin theta
r=square root of x^2 + y^2
theta=tan^-1(y/x)


So I guess I am going to work a few examples nowww.




EXAMPLE 1: convert (3,4) into polar form.

• r=square root 3^2 + 4^2=5


• theta=tan^-1(4/3)=53.130 and 233.130


• so your answers are (5, 53 degrees 7 minutes 48 seconds) and (-5, 233 degrees 7 minutes 48 seconds)

EXAMPLE 2: plot the points (-4, 10 degrees)

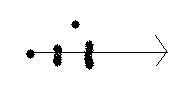
OKAY, well that is it for this weeek.
-Brad.

11-2

This week I am going to explain how to work problems in 11-2, which are problems using complex numbers. There are a few formulas in this section. These formulas are:

• z=x+yi
• z=rcos theta + rsin theta i
• z=rcis theta
• |z|=square root of x^2 + y^2

Note: To multiply complex numbers:

• With rectangular problems remember to always foil.
• With polar problems you will multiply r and add theta.

Now I am going to do a few examples to help you understand how to work these problems.

Example 1: -1 + i

• Since it is in rectangular form, you are going to find r and theta.
• r=square root of -1^2 + 1^2. Which equals square root of 2.
• theta=tan^-1(-1). Which equals 45.
• When you put that on the quadrants, you will get 135 and 315.
• So once you do that, your answers will be square root of 2 cis 135 degrees and -square root of 2 cis 315 degrees.

Example 2: 6 cis 100 degrees

• x=6 cos 100= -1.042
• y=6 sin 100= 5.909
• Your answer is going to be -1.042 + 5.909

Well, that is all for this week. BYEEE

--Halie